 Elektotehnički fakultet, Univerzitet u Beogradu
Elektotehnički fakultet, Univerzitet u Beogradu
 Elektotehnički fakultet, Univerzitet u Beogradu
Elektotehnički fakultet, Univerzitet u Beogradu
Ako je n prirodan broj ili nula može se definisati funkcija
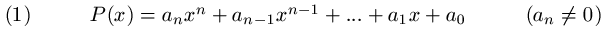
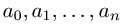 realni brojevi. Ovo je polinom ili polinomska funkcija
stepena n. Ona je definisana za svako
realni brojevi. Ovo je polinom ili polinomska funkcija
stepena n. Ona je definisana za svako 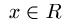
Polinomi su, sa računarske tačke gledišta, najjednostavnije funkcije, jer se njihova vrednost može izračunati u svakoj tački, samo primenom osnovnih operacija.
Za svaki polinom P stepena n oblika (1) postoji tačno n kompleksnih (ili realnih) brojeva 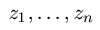 takvih
da je
takvih
da je
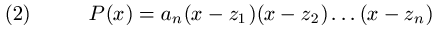 za svako
za svako 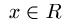
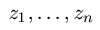 nazivamo korenima ili
nulama polinoma P. Očigledno je
nazivamo korenima ili
nulama polinoma P. Očigledno je  za svako i = 1, ..., n
za svako i = 1, ..., n
Među korenima može biti međusobno jednakih brojeva. Ako se broj z pojavljuje r puta kao koren polinoma, kažemo da je to koren reda r.
Dakle, korenu reda r odgovara u faktorizaciji (2) faktor oblika 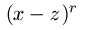 .
.
Koreni čiji je imaginarni deo različit od nule (tzv. imaginarni koreni) pojavljuju se u parovima: ako je 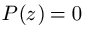 , onda je
i
, onda je
i 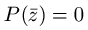 . Dakle, paru imaginarnih korena reda s
. Dakle, paru imaginarnih korena reda s 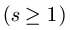 odogovara faktor
odogovara faktor 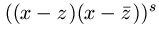 .
Ako stavimo da je
.
Ako stavimo da je 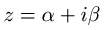 ,
, 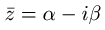 , dobijamo da je
, dobijamo da je
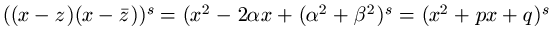
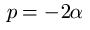 ,
, 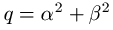 , pa je
, pa je 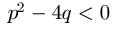 .
.
Prema tome, faktorizacija (2) može se zapisati u obliku:
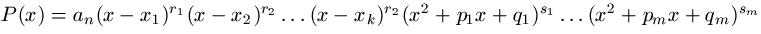
 realni koreni reda
realni koreni reda  respektivno, a ostali odgovaraju kompleksnim korenima.
respektivno, a ostali odgovaraju kompleksnim korenima.
© Milan Branković, Napravljeno pomoću alata GeoGebra