Elektotehnički fakultet, Univerzitet u Beogradu
Elektotehnički fakultet, Univerzitet u Beogradu
Najpoznatiji oblik linearne funkcije je: y = kx + n (eksplicitni). Problem sa ovom definicijom je da funkcije ovog oblika (uprkos njenom imenu), ne zadovoljavaju
obavezno uslov linearnog preslikavanja, ukoliko je k jednako nula. Grafik ove funkcije je prava. K je koeficijenat pravca, odnosno k =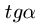 
gde je 
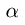- ugao koji prava gradi sa pozitivnim smerom x-ose, n - je odsečak na y-osi.
Nula funkcije je mesto gde grafik seče x-osu, a dobija se kad stavimo y = 0, pa izračunamo koliko je x .
Ako je k>0 funkcija je rastuća i sa pozitivnim smerom x-ose gradi oštar ugao, a ako je k<0 funkcija je opadajuća i sa pozitivnim smerom x-ose gradi tup ugao. Na grafiku, menjanje parametra k čini liniju strmijom ili ravnijom, a menjanje parametra n pomera liniju gore ili dole.
Funkcija je pozitivna za y>0 tj. kx + n > 0 i grafik je iznad x-ose. Funkcija je negativna za y<0 odnosno kx + n < 0 i grafik je ispod x-ose.
© Milan Branković, Napravljeno pomoću alata GeoGebra