Home page
Problems related to the solvability of
polynomial equations
Finite
solvability of polynomial equations
The polynomial system
of equations:
has a finite number
of solutions if and only if any Groebner basis of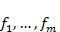 
has the following
property:
For every variable 
, there exists a
polynomial such that its leading term with respect to the chosen term ordering
ia a power of 
The number of solutions is equal to the cardinality of
the set of monomials that are no multiples of the leading monomials of the
polynomials in the Groebner basis.
|
Polynomials are entered as the sum of terms.
For every term, first must enter coefficient and then
enter every variables and their power. Every variable must be entered in the brackets,
and before power of variable must be entered char ^. |