Problemi vezani za rešivost sistema jednačina
Problem
konačne rešivosti sistema jednačina
Neka je dat sistem
polinomskih jednačina:
za neke polinome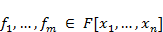 
. Formirajmo ideal 
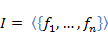u zatvorenom polju F i njegovu Grebnerovu bazu
G. Sledeći uslovi
su međusobno ekvivalentni:
1.
Sistem
jednačina 
ima
konačan broj rešenja.
2.
.
3.
Vektorski
prostor 
je
konačnodimenzionalan.
Broj rešenja je jednak broju monoma koji nisu deljivi sa
vodećim monomima iz Grebnerove baze G.
Polinomi se unose kao suma termova. Za svaki term se prvo unosi koeficijent (ukoliko je on jednak 1 ne mora se uneti) i zatim svaka promenljiva i njen stepen.
Važno je da se svaka promenljiva unosi u zagradama, a pre samog stepena unosi se znak ^.